Advanced Mathematics for Engineers 1
Advanced Mathematics for Engineers 1 (Hochschule Ravensburg-Weingarten Univ.). Instructor: Professor Wolfgang Ertel. After a repetition of basic linear algebra, computer algebra
and calculus, this course will deal with numerical calculus, statistics and function approximation, which are the most important basic mathematics topics for engineers in the fields of
computer science, mechatronics and electrical engineering.
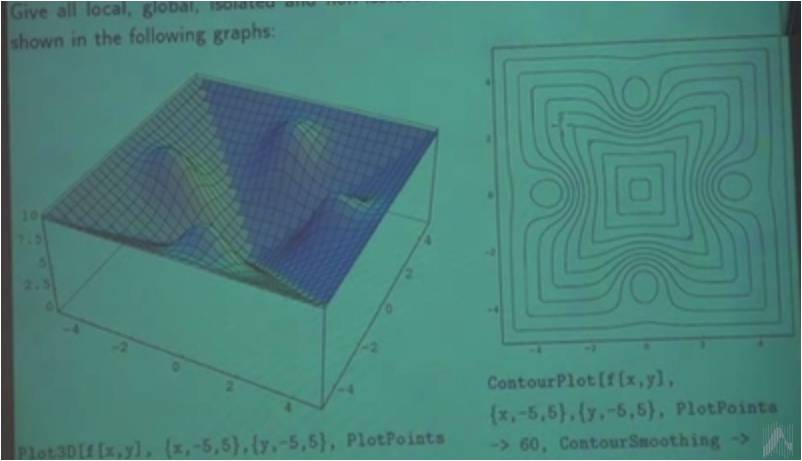
Topics covered in this course, Advanced Mathematics for Engineers 1, include: computer algebra; calculus including sequences, power series, continuity, Taylor series, and differential calculus
in many variables; discrete distributions; roots of nonlinear equations, and method of least squares and pseudoinverse.
 |
| References |
| Advanced Mathematics for Engineers | Hochschule Ravensburg-Weingarten Instructor: Professor Wolfgang Ertel. Demos and Course Material. Octave Exam Programs. Previous Examinations. Video Lectures from Previous Semesters. |